Contents
Introduction of Marginal Analysis
The term marginal can be defined as a change in total quantity due to one unit change in its determinant. Thus, marginal analysis is a microeconomic concept that deals with a small change in given economic variables or changes in the economic variables due to unit changes in their determinants. Marginal analysis in economics is considered one of the helpful decision-making tools that help consumers as well as businesses to make decisions regarding the allocation of their scarce resources with minimizing cost and maximizing benefits.
The concept of marginal is used in utility analysis (relating to the decision of utilizing further one unit), production analysis (relating to the decision of further one unit of production), cost analysis (determining the cost of additional unit), and revenue analysis (determining the revenue associated with additional one unit of sale). This concept is thus used in the theory of the firm to determine the profit-maximizing level of output. For example, the concept of marginal revenue and marginal cost is used to determine the optimum level of output by the producer.
Marginal revenue is the change in total revenue due to one unit change in the number of sales.
Symbolically, MRn=TRn-TRn-1 (If n= 10, n-1= 9)
Where MR= Marginal revenue and TRn=Total revenue from the sale of n units of output.
Similarly, marginal cost is the rate of change in total cost due to one unit change in the quantity output.
Symbolically, MCn=TCn-TCn-1 (If n= 10, n-1= 9)
Where MC= Marginal cost TCn =Total cost of producing n units of output
The Decision Rule
After the calculation of marginal values, the economic agent now can take economic decisions by using such marginal values. For example, a profit-maximizing firm takes a production decision based on marginal analysis. A firm continues to expand its production until the Marginal Revenue will be greater than the Marginal Cost i.e. MR>MC. When the marginal revenue will become lower than the marginal cost (i.e. MR<MC), then the producer will stop producing and avoid losses.
Example of Use of Marginal Analysis
Thus the level of output where marginal revenue is equal to marginal cost is the point of maximum profit. Here marginal analysis works as the guideline to take the decision relating to economic activities of production. The following table shows an example of it:
| Output (Q) | Total cost | Total revenue | Marginal cost | Marginal revenue | Total profit |
| 0 | 0 | 0 | – | – | – |
| 1 | 10 | 100 | 10 | 100 | 90 |
| 2 | 30 | 180 | 20 | 80 | 150 |
| 3 | 60 | 240 | 30 | 60 | 180 |
| 4 | 100 | 280 | 40 | 40 | 180 |
| 5 | 150 | 300 | 50 | 20 | 150 |
From the table, we see that when the number of output increases, both total cost and total revenue also increase. Marginal revenue is continuously decreasing with an increase in output. The value of profit is initially increasing with the expansion of output but this is not the case forever. After a certain level of output, the profit starts to fall even if there is an expansion of output. Thus to produce optimum output or profit-maximizing output we can take the help of marginal analysis. Here marginal revenue and marginal cost are equal where the total profit is maximized. Thus, to maximize the profit or to produce profit-maximizing output marginal revenue and margin costs are needed for a producer.
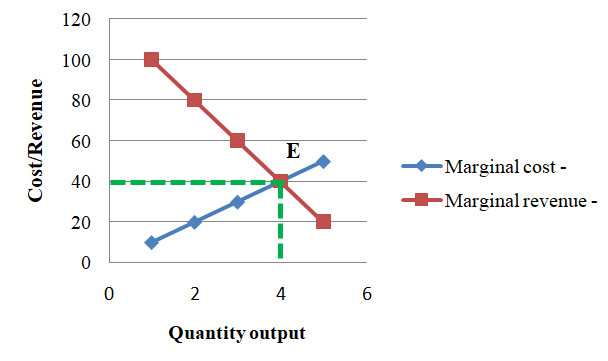
In the figure, MR is a marginal revenue curve that is downward sloping. That means as the number of goods X increases, the revenue of the next unit (marginal revenue) falls. Similarly, MC is the marginal cost curve which is upward in slope. It means at the quantity of output of X good is increased then the cost of the next unit (marginal coat) will also increase. Both curves are equal to each other at point E where MC equals MR and the firm is in equilibrium as it attains the maximum profit.
Conclusion
Marginal analysis which comes under microeconomic theory plays a prominent role in economic analysis. This one is a useful decision-making tool that helps individuals and businesses to make efficient decisions relating to the allocation of scarce resources. Therefore the concept of marginal analysis has a greater role in economics and for economic agents.
References and Suggested Readings
Dhakal, R. (2019). Microeconomics for Business. Kathmandu: Samjhana Publication Pvt. Ltd.
Shrestha, P.P. and et.al. (2019). Microeconomics for Business. Kathmandu: Advance Sarswati Prakashan.