Concept of Optimum Employment of Input

Every producer engages in the act of production to earn possible maximum profit by utilizing the available amount of total cost outlay, prices of factors of production, state of technology, governmental policy, and so on. To ensure a maximum profit or to minimize the cost of production, the selection of an efficient combination of factors of production is vital. If the employment of factors of production is efficient then it can generate possible maximum profit from the production. This article attempts to explain the procedure of employment of an efficient combination of factors of production in the short run. In the short run, only one factor is assumed to be variable, and others are assumed to be fixed, thus optimum employment of single variable input or employment of one variable input is a short-run phenomenon. Similarly, in the long run, the employment of two variable inputs is suitable to discuss. Here, we will only explain the optimum employment of single variable input.

Meaning of Optimum Employment of Single Variable Input

The optimum employment of input refers to the decision of resource allocation to maximize output at a given level of cost or to minimize the total costs at a given level of output.  It guides a producer in deciding how to allocate available scarce budget/outlay to hire or purchase a profit-maximizing combination of factors of production/inputs. Optimum employment of single or one variable input is the case of the short-run in which only labor is changed assuming all the other factors of productions are fixed.

Optimum Employment/Use of Single Variable Input

It is the case of a short-run production function where only labor is variable input and capital remains fixed. So, the output can be changed by changing the employment of labor only.

This guides a producer to decide the profit-maximizing number of labor employment, keeping capital fixed. It means that this explains how much labor should be employed by a business firm to maximize the level of profit. Therefore, it gives criteria that the firm should hire labor units until the marginal revenue productivity of labor would become equal to the marginal cost of hiring labor.

Assumptions

The optimum employment of single variable input is based on the following assumptions.

• The firm is using a single variable input (labor)
• The goal of the firm is to maximize profit
• The firm produces a single commodity
• There exists perfect competition in both products as well as factor markets.
• The price of the product is fixed
• The state of technology remains unchanged
• The economy operates at fuller employment
• There is the operation of the law of diminishing returns
• Labor units are homogenous and divisible 

Equilibrium Condition/Condition Required for Optimum Employment of Single Variable Input

Based on the above assumptions, the firm can accomplish its objective of profit maximization and ensures its equilibrium at the point where demand for labor and supply of labor becomes equal. Thus, the equilibrium condition is

            Demand for Labour = Supply of Labour

            or 𝐷_𝐿=𝑆_𝐿

Demand for Labour (𝑫_𝑳)

In the case of a perfect competition market, the marginal revenue product of labor (𝑀𝑅𝑃𝐿) curve is the demand curve for labor.

𝑀𝑅𝑃_𝐿 is a change in total revenue due to one additional unit of labor employment. In the case of a perfectly competitive market, 𝑀𝑅𝑃𝐿 is equal to the value of marginal productivity of labor (𝑉𝑀𝑃_𝐿).

𝑀𝑅𝑃_𝐿=𝑀𝑃_𝐿×𝑀𝑅 𝑜𝑟 𝑃 [In a perfectly competitive market MR=P so, 𝑀𝑅𝑃_𝐿=𝑉𝑀𝑃_𝐿]

The 𝑀𝑅𝑃_𝐿 curve slopes downward because the value of 𝑀𝑃𝐿 declines with an increase in a unit of labor. If we multiply the declining value of marginal productivity of labor by a constant price, then the resulting value will also decline. Thus, the resulting value is 𝑀𝑅𝑃𝐿 and thus it declines with additional employment of labor.

Supply of Labour (𝑺_𝑳)

We assume that the factor market is perfectly competitive thus wage rate remains unchanged. Due to the constant wage rate, the supply curve of labor is parallel to X-axis or is horizontal. The supply of labor represents the marginal cost of labor which is also called marginal expenditure as the wage rate is constant. Thus

𝑀𝐶_𝐿=ME=𝑊 

Now for the equilibrium condition of a firm or for the maximization of profit or to find the number of profit-maximizing labor or optimum employment of single variable input, the required condition is 𝐷_𝐿=𝑆_𝐿

It means 𝑀𝑅𝑃_𝐿=𝑀𝐶_𝐿 OR 𝑀𝑅𝑃_𝐿= 𝑊 

It is the required condition to determine the optimal number of labor employment in the case of the single variable input. It can be explained with the help of the following diagram.

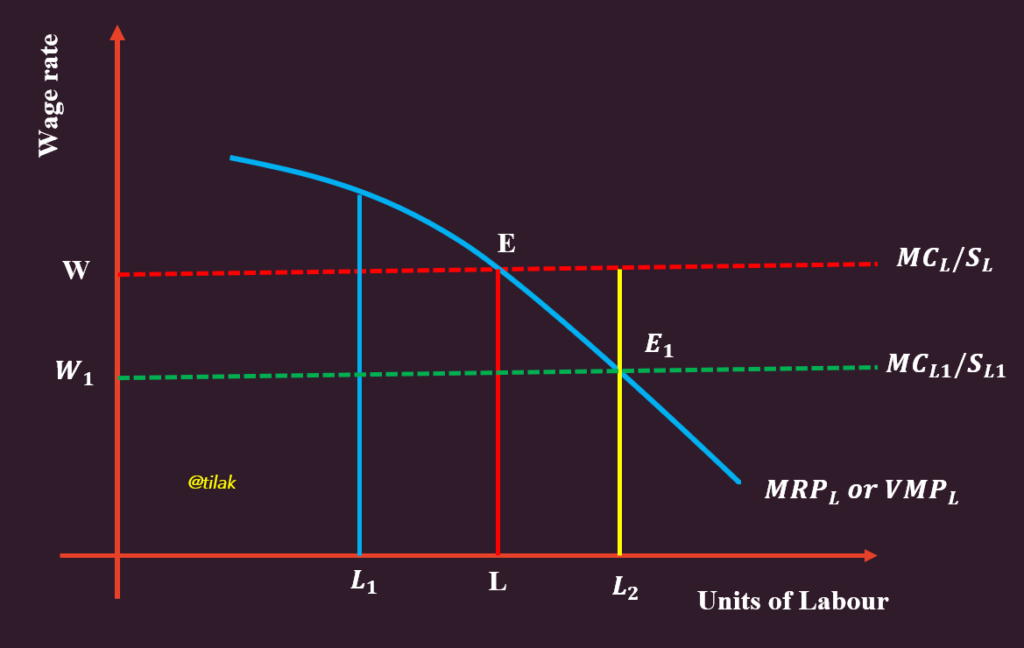
The above figure shows the optimum employment of single variable input that is optimum employment of labor.  At point ‘E’ the equilibrium condition is obtained, and the OL unit of labor is employed by the firm. If the firm employs labor more than OL at the OW wage rate, it must suffer a loss, and employment of less than OL units of labor at the same wage rate also results in the loss of the opportunity to earn more.

Thus, at the given wage rate, OL employment of labor makes marginal revenue from labor exactly equal to marginal expenditure or wage rate and the rational producer does not hire more or fewer labors than OL units. More employment of labor (𝐿2) is desirable only when the wage rate falls from W to 𝑊1. If the wage rate increases the rational producer will not be able to hire even OL units of labor.

Conclusion

In this article, we have explained the mechanism explaining the optimum employment of single variable input. Assuming both products, as well as factor markets, are perfectly competitive, the optimum employment of one variable factor is given by equality between the marginal revenue productivity of the factor and the marginal cost of hiring additional units of the same factor. In the case of labor employment, the optimum number of labors can be found by hiring that number of labors which equalizes the marginal revenue productivity and wage rate. 

Mathematical Problem

The production function of the firm is Q=98L-3L². The firm can sell its output at Rs. 30 and it hires whatever labor wants at Rs. 60 per day. Determine optimum employment of single variable input labor.

Solution

Here given

Production function (Q) = 98L-3L²

Price of the product (P) = Rs. 30

Wage rate (W) = Rs. 60

The question is seeking the number of profits maximizing units of labor. The profits maximizing or optimum employment of single variable input requires the fulfillment of equilibrium condition that is equality between marginal revenue productivity of labor and wage rate. Thus, it can be expressed as below.

MRP_L = ME or wage rate

Here

MRP_L = MP_L×MR (P)

MPL=d(Q)/d(L) = d(98L-3L²)/dL = 98-6L

Therefore, MRP_L = (98-6L)30 = 2940-180L

Now

2940-180L=60

L= (2940-60)/180= 16 Units

Therefore, the optimum employment or single variable input (labor) is 16 units. It means 16 units of labor employment ensures the maximum profit for the firm.