Introduction

German economist H.H. Gossen developed his second law as the law of substitution or the law of equi-marginal utility/the law of maximum satisfaction in 1854 AD. This law is further developed and popularized by Prof. Alfred Marshall.

According to this law, the consumer allocates her/her limited money income among various goods for getting maximum satisfaction and the consumer gets maximum satisfaction only when s/he obtains equal marginal utilities from the consumption of different commodities.

Thus, the law of substitution states that a consumer spends his/her limited income on two or more goods in such a way that the ratio of marginal utility to the price of each commodity should be equal and should be equal with the marginal utility of money. This is called the proportionality rule.

Algebraically, it can be stated

𝑴𝑼𝒙/𝑷𝒙 = 𝑴𝑼𝒚/𝑷𝒚 = 𝑴𝑼m

Where

MU_X= Marginal utility derived from X-commodity; MU_Y= Marginal utility derived from Y-commodity; P_X= Price of commodity-X; P_Y= Price of commodity-Y; MU_m is Marginal utility of money

For more than two commodity cases, the required condition is

𝑴𝑼𝒙/𝑷𝒙 = 𝑴𝑼𝒚/𝑷𝒚 =…. = 𝑴𝑼n/𝑷n= 𝑴𝑼m

Where MU_n is marginal utility derived from nth commodity and P_n is the price of the nth commodity.

If 𝑴𝑼𝒙/𝑷𝒙>𝑴𝑼𝒚/𝑷𝒚= 𝑴𝑼m the consumer increases consumption of commodity-X until the ratio of marginal utility to the price of two goods are equal as 𝑴𝑼𝒙/𝑷𝒙 = 𝑴𝑼𝒚/𝑷𝒚= 𝑴𝑼m and attains equilibrium. On the contrary, if 𝑴𝑼𝒙/𝑷𝒙<𝑴𝑼𝒚/𝑷𝒚= 𝑴𝑼m, the consumer increases consumption of commodity-Y until 𝑴𝑼𝒙/𝑷𝒙 = 𝑴𝑼𝒚/𝑷𝒚= 𝑴𝑼m and attains equilibrium.

This indicates that consumer continuously substitutes one commodity having higher marginal utility for another commodity having lower marginal utility until it becomes equal. Hence, this law is called the law of substitution. 

Assumptions

This law is based on the following assumptions

• Cardinal measurement of utility
• Consumers are rational
• The income of the consumer remains constant
• The marginal utility of money remains constant
• Prices of the commodities remain constant 
• Commodities are divisible into small units
• Consumption takes place at a given time

Based on the above assumptions, the law can be explained with the help of the following table and graph.

Suppose that a consumer wants to spend Rs. 40 on the purchase of commodity X and Y, the prices of which are Rs. 5 and Rs. 10, respectively. The table below depicts the marginal utilities of these two goods X and Y. 

Units	MUX (Utils)	MUY (Utils)	MUX/PX (Utils)	MUY/PY (Utils)
(1)	(2)	(3)	(4)	(5)
1	50	80	10	8
2	45	70	9	7
3	40	60	8	6
4	35	50	7	5
5	30	40	6	4
6	25	30	5	3

Observing the above table, columns (2) and (3) give marginal utility of X and Y. Columns (4) and (5) give the ratios of marginal utility to the price of two commodities (marginal utility of a rupee spent on the purchase of two goods).

Marginal utility per rupee spent on each good diminishes, which occurs because the marginal utility of each good diminishes as we consume more of it.

From the table, the condition 𝑴𝑼𝒙/𝑷𝒙 = 𝑴𝑼𝒚/𝑷𝒚 can be fulfilled at many points, such as 3X and 1Y, 4X and 2Y, 5X and 3Y, 6X and 4Y.

To purchase these different combinations of X and Y, the consumer will be required to inure different amounts of expenditure as shown in the following table.

Combinations	Total Expenditure
(1)	(2)
3X+1Y 4X+2 Y4X+3Y 6X+4Y	Rs. (3*5+1*10=25) Rs. (4*5+2*10=40) Rs. (5*5+3*10= 55) Rs. (6*5+4*10= 70)

Since the consumer must spend Rs. 40 on the purchase of good X and Y. If he purchases combination (i), s/he will be able to spend Rs. 25 only. If he purchases combination (iii) and (iv), s/he is required to spend Rs. 55 and Rs. 70 respectively, which are out of his reach, given the budget.

It is only when s/he purchases combination (ii) that s/he will be able to acquire an expenditure of Rs. 40. Thus, the consumer is in equilibrium when s/he buys 4 units of X and 2 units of Y and thereby spends a sum of Rs. 40. So, the consumer’s equilibrium condition is when MUx/Px= MUy/Py; and at the same time, the consumer must spend the entire income on the purchase of the two commodities.

For determining total utility that consumer has obtained from his/her income of Rs. 40, we can add the marginal utilities obtained from the purchases of each product. Referring to the table, we can see the marginal utilities for the first four units of good X are 50+45+40+35= 170 utils. Similarly, the marginal utilities for the first two units of Y are 80+70= 150 utils.

When 4 units of X and 2 units of Y are purchased, the consumer will obtain 170+ 150= 320 utils of utility. No other combinations of X and Y can give this much utility when income is Rs. 40.

This can be explained with help of the following diagram. 

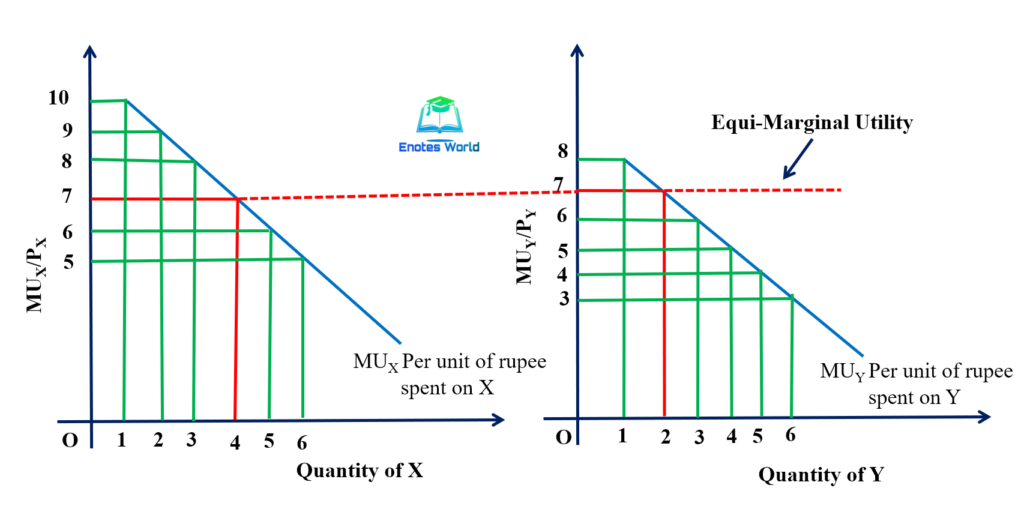
𝑴𝑼𝒙 curve in Panel (i) shows the marginal utility per unit of rupee spent on commodity X corresponding to different units of X, 𝑴𝑼𝒚 curve in Panel (ii) shows the marginal utility per unit of rupee spent on commodity Y.  

These two curves are negatively sloped because of the diminishing marginal utilities of each good. It is cleared from the graph that when the consumer buys 4 units of commodity X and 2 units of commodity Y, 𝑴𝑼𝒙/𝑷𝒙 = 𝑴𝑼𝒚/𝑷𝒚 is equal to 7 utils. The dotted line in the graph shows equal marginal utility (7 utils) from the last unit of rupee spent on both goods.

Conclusion

The Law of substitution states that the rational consumer should distribute his/her limited income among several goods in such a way that the last unit of money spent on each commodity ensures him/her the same marginal utility and which is also equal to his/her marginal utility of money. For a consumer to be in equilibrium, s/he must obtain the condition MUx/Px=MUy/Py; and at the same time, the consumer must spend all the income on the consumption of the two commodities. Therefore, consumers continuously substitute one good for another (Say good X for good Y) until MUx/Px becomes equal to MUy/Py. Once if s/he obtains the condition MUx/Px=MUy/Py=MUm then s/he will stop further substitution and gain the maximum satisfaction.

Limitations/Exceptions to the Law of Substitution

• It is difficult to know marginal utilities from different commodities because they cannot be measured.
• In many cases, consumers may be guided by habits and customs and therefore their decisions regarding purchasing different commodities are directed more by these considerations rather than economic considerations.
• Many consumers are ignorant and so, they may not be able to arrive at the equilibrium position due to their ignorance.
• In the case of expensive and indivisible commodities like cars, refrigerators, etc. it is not possible to equate the marginal utility of a rupee spent on the purchase of a car or a refrigerator. Thus, this law is not applied in the case of goods that are not divisible into small units.
• In real life utility obtained from different commodities is not independent as goods are substitutes or complements.
• When there is a change in tastes, preferences, fashions, etc. due to different factors such as the size of the population, social and economic conditions, etc.