Meaning of Consumer’s Equilibrium

Consumer’s equilibrium is the position in which the consumer reaches the highest level of satisfaction given his or her money income and the prices of goods. It means a consumer is said to be in equilibrium when he/she can maximize his/her utility with the given limited resources. At the consumer’s equilibrium point the consumer spends all his/her income between different goods and services and derives maximum pleasure. In marginal utility theory, the consumer is in equilibrium with the combinations of goods purchased based on marginal utility (MU) and price (P) that maximize the total utility.

Here, under the topic of consumer’s equilibrium, we try to answer the question of how a consumer allocates his money income to the various goods and services he consumes to reach his equilibrium. Thus, in this article, we will explain how a consumer attains equilibrium or how a consumer’s equilibrium under cardinal utility analysis is attained under two different cases.

Assumptions

The analysis of consumer’s equilibrium is based on the following assumptions

Rationality: It is assumed that consumer is rational in the sense that while consumer goods and services; he tries to maximize his satisfaction from his limited resources.

Limited Money Income: The consumers have a limited money income to spend on the purchase of goods and services.

Maximization of Pleasure: Every rational consumer desires to maximize his happiness or utility from his money income. It means he selects the goods and expends his income in such a way that his total utility is optimum.

Cardinal Utility: The utilities derived from goods and services can be calculated and expressed in numbers. Thus, utility is considered a cardinal concept.

Diminishing Marginal Utility: If a consumer consumes the successive units of the commodity one after another, the satisfaction which is derived from the additional units of the commodity goes on diminishing.

Constant Marginal Utility of Money: The marginal utility of money remains constant whatever the level of consumer’s income and each unit of money has utility equal to one.

The utility is Additive: Cardinal school of utility analysis believes that utility derives from different goods can be added up. It can be expressed through the utility function. So the total utility can be obtained by adding the utilities obtained from the individual commodities. It can be expressed as;

TU= U₁ (X₁) +U₂ (X₂) +…. +U_n (X_n)

Consumer’s Equilibrium: Single Commodity Case

Here we illustrate the consumer’s equilibrium by taking a simple one commodity case (Consumer’s Equilibrium under Cardinal Utility Analysis and case of single commodity). Suppose that a consumer with a certain income given money income consumes only one commodity X. The relevant issue is how much quantities of good X should be consumer purchase at its given price to reach the equilibrium. The answer to this issue is that the consumer should purchase that much quantity of the commodity at its given price and given income so that he can maximize the total utility from his purchase.  

In this regard, a utility-maximizing consumer will be in equilibrium when he or she purchases that much quantity of the commodity where the marginal utility of the commodity equals its price. Both the amount of money (price) that the consumer has to spend to purchase a unit of the commodity and the commodity both give him utility so he either can spend the money on the purchase of the commodity or keep it with himself. If the marginal utility of a commodity is greater than the marginal utility of money which the consumer has to give for the purchase of a unit of commodity, a utility-maximizing consumer will purchase the commodity in exchange for money.

It means the consumer man maximizes total utility by purchasing more units of the commodity at its lower price. Thus, if the marginal utility of X is greater than the price of X (MU_X>P_X), the consumer can increase his or her satisfaction by purchasing more units. Likewise, if the marginal utility of X is less than its price (MU_X <P_X), the consumer can increase his or her total utility by consuming less of goods X. Thus, he will maximize total utility if the marginal utility of a commodity equals its price.

Symbolically, the consumer’s equilibrium condition under the single commodity case can be expressed as;

MU_X=P_X 

Where MU_X is the marginal utility of commodity X and P_X is the price of commodity X.  

This concept is more clearly understood with the help of the following table or hypothetical example.

Unit of T-shirt	Marginal Utility
1	700
2	650
3	600
4	500
5	350

Suppose that a consumer wants to purchase a T-shirt. He gets utility (measures in terms of money) from different units of T-shirts as displayed by the above table. From the table, we can say that the consumer gets marginal utility equal to Rs. 700 from the first T-shirt. As he consumes extra units of T-shirts, the marginal utility does on diminishing.  Suppose the price of the T-shirt is Rs. 600. Here the consumer will be in the equilibrium when he purchases 3 T-shirts as the marginal utility of the third T-shirt (Rs. 600) is equal to the price of the T-shirt (Rs. 600).  

The following figure shows consumer’s equilibrium under cardinal utility analysis in the case of a single commodity case.

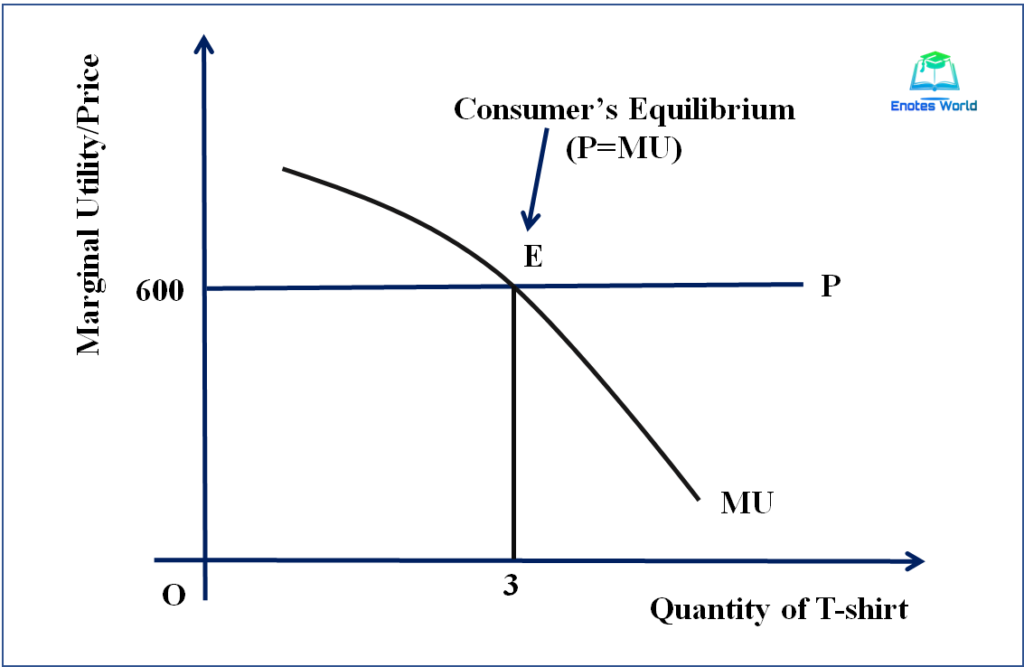
In the above figure, MU is the marginal utility curve of the T-shirt in terms of money. The downward slope of such a curve indicates the law of diminishing marginal utility. The horizontal straight line P shows the price of a T-shirt. The MU curve and the price line P intersect to each other at point E. thus, the consumer is in equilibrium, at point E, where the MU= P. In our above hypothetical example, this condition is fulfilled when the consumer purchases 3 T-shirts. At any point above E, MU>P and at any point below E, MU<P. Thus, the consumer can therefore increase his satisfaction by reducing the purchased quantity below point E and by increasing the purchase of more units. So, point E is the equilibrium where the MU of T-shirt in terms of money is equal to the price of the T-shirt. 

Consumer’s Equilibrium: Two Commodity Case

In reality, consumers have to buy several goods and services with their limited income. The budget constraint curbs the amount of total utility that can be obtained by purchasing various commodities. So, here we will illustrate the consumer’s equilibrium under cardinal utility analysis in the case of two commodities. A consumer will be at equilibrium when he/she allocates his/her given income on the purchase of different goods in such a way that he/she maximizes his/her total utility from his/her expenditure on different goods. The law of equi-marginal utility is of great help in solving the problem of consumer’s equilibrium in two commodity case.

According to the law of equi-marginal utility, the utility-maximizing consumer must allocate his/her income among various goods in such a way that the last unit of money spent on each of the goods gives him/her equal marginal utility.

We can explain the theory and mechanism of attainment of equilibrium under two commodity cases with the help of a hypothetical example.

The marginal utility of rupees we spend on a good equal to the marginal utility of the good divided by the price we pay for it. Suppose MU_X denotes the marginal utility of the last unit of commodity X, P_X denotes its price, then marginal utility per rupee spent on X is MU_X/P_X.  

For instance, if a consumer buys 4 units of good X and the marginal utility from the 4^th unit is 35 utils and the price of X is Rs. 5, the marginal utility per rupee is 35/5=7 utils.

Similarly, MU_Y/P_Y (where MU_Y is the marginal utility from the last unit of commodity Y, and P_Y is the price of Y) will indicate the marginal utility per rupee spent on Y.

Suppose, a consumer spends his income on the purchase of only two goods X and Y. To understand why a consumer maximizes his/her total utility when the marginal utility of the last rupee spent on each good is equal, consider a consumer who receives greater marginal utility from a rupee spend on X than from a rupee spent on Y. Furthermore, the last rupee spent on X yields utility equal to 5 utils whereas the last rupee spent on Y gives him 3 utils of utility. In such a case, the total utility can be increased by switching one rupee from commodity Y to commodity X and gaining the difference between the utility of the last rupee spent on each, i.e., by 2 units (5-3=2). Thus total utility will increase.

The utility-maximizing consumer will continue to switch his expenditure from Y to X brings him more utility than a rupee spent on Y. But this transfer of expenditure from Y reduces the quantity of Y consumed and, given the law of diminishing marginal utility, raises the marginal utility of good Y. at the same time the quantity consumed of X increases and thereby, following the law of diminishing marginal utility, the marginal utility of X falls.   

This process of reallocation of expenditure will ultimately lead to equalization of the marginal utility of the last rupee spent on each of the two goods.  At this point, the consumer will not gain anything by a further reallocation of expenditure from commodity Y to commodity X.

From our above explanation, we can say that the consumer will be in equilibrium while purchasing X and Y, when

MU_X/P_X=MU_Y/P_Y=MU per unit of money

Here, MU_X/P_X shows the marginal utility of a unit of money (rupee) spent on commodity X. Similarly, MU_Y/P_Y indicates the marginal utility of a unit of money spent on commodity Y.

This law can be illustrated by the law of equi-marginal utility by taking a numerical example. For simplicity, we assume that a consumer wants to spend Rs. 40 on the purchase of commodity X and Y, the prices of which are Rs. 5 and Rs. 10 respectively. The following table shows the marginal utilities of these two goods X and Y;

Units	MUX	MUY	MUX/PX	MUY/PY
(1)	(2)	(3)	(4)	(5)
1	50	80	10	8
2	45	70	9	7
3	40	60	8	6
4	35	50	7	5
5	30	40	6	4
6	25	30	5	3

In the above table columns, 2 and 3 give marginal utility of X and Y. column 4 and 5 give the ratios of marginal utility to the price of the two commodities, i.e., the marginal utility of a rupee spent on the purchase of two commodities. The table also shows that the marginal utility per rupee spent on each good diminishes, which occurs because the marginal utility of each good diminishes as the consumers consume more of it.

Now the quantities of good X and Y to determine consumer’s equilibrium point, the marginal utility per rupee will be quite useful, from the table, MU_X/P_X=MU_Y/P_Y=MUm can be fulfilled at any points such as 3 units of X and 1 unit of Y, 4 units of X and 2 units of Y, 5 units of X and 3 units of Y, 6 units of X and 4 units of Y. To purchase these different combinations of X and Y the consumer has to incur a different amount of expenditure as shown in the following table;

Combinations	Total Expenditure
3 units of X + 1 unit of Y	Rs. 25 (3*5+1*10)
4 units of X + 2 units of Y	Rs. 40 (4*5+2*10)
5 units of X + 3 units of Y	Rs. 55 (5*5+3*10)
6 units of X + 4 units of Y	Rs. 70 (5*6+4*10)

The consumer has to spend Rs. 25 on the purchase of fist combination, Rs. 40 on the purchase of the second combination and similarly Rs. 70 in the purchase of the fourth combination. We have assumed that the consumer has Rs. 40 and he is allowed to spend Rs. 40 only so the consumer will be in equilibrium when he/she buys 4 units of X and 2 units of Y and thereby spends a total sum of Rs. 40. We can generalize equilibrium condition as; consumer’s equilibrium will be when MU_X/P_X=MU_Y/P_Y and at the same time, the consumer must spend the entire income on the purchase of the two commodities.

The total utility that consumer obtains from his/her income of Rs. 40  is 320 utils including (50+45+40+35)170 utils from good X and (80+70) 150 utils from good Y. No other combination of good X and Y can give as much utility when income is Rs. 40.

The following diagram also helps us to understand the consumer’s equilibrium in the case of two commodities.

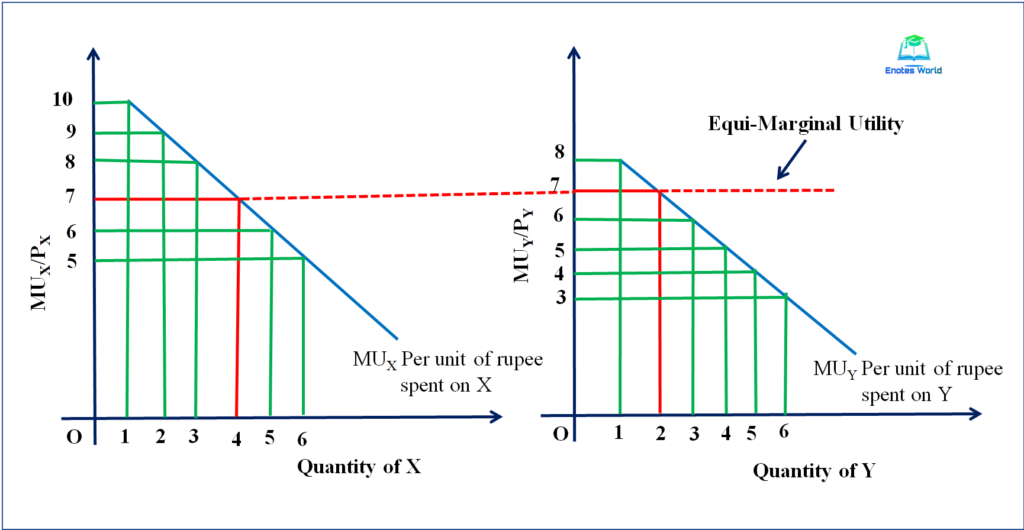
In the above two panel diagrams, units of good X have measured on the horizontal axis in panel-I and units of Y have shown on the horizontal axis in panel-II. MU_X/P_X and MU_Y/P_Y are on the vertical axis in panel-I and panel-II respectively. MU_X in panel shows marginal utility per unit of rupee spent on good X corresponding to its different units. Similarly, the MU_Y curve in panel-II shows the marginal utility per unit of rupee spent on commodity Y corresponding to different units of Y.

Curve MU_X and MU_Y are negatively sloped due to the operation of diminishing marginal utility. The linear MU curve is drawn to indicates the equilibrium quantities of good X and Y. From the diagram, we can see that at 4 units of commodity X and 2 units of commodity Y, MU_X/P_X=MU_Y/P_Y =MUm=7. So the dotted line in the diagram shows equal marginal utility (7 utils) from the last unit of rupee spent on both of the goods. It fulfills both of the conditions for attaining equilibrium in the case of tow commodities and the consumer has attained maximum satisfaction.

References and Suggested Readings

Ahuja, H.L.(1970). Advanced Economic Theory. Delhi: S Chand and Company Limited

Dwibedi, D.N. (2003). Microeconomics Theory and Applications. Delhi: Vikas Publishing House Pvt. Ltd.

Kanel, N.R. and et.al (2016). Microeconomics. Kathmandu: Buddha Publications

Mankiw, N.G. (2009). Principles of Microeconomics. New Delhi: Centage Learning India Private Limited