Contents
Concept of Price/Budget Line or Budget Constraint
The indifference curve displays the preference of the buyer. To find out the unit of two goods or quantity of two goods purchased by the household, we should know how much expenditure the household wants to sustain on these two goods and what are the prices of two goods. The capacity of individual buyers to expense on two commodities and their prices will qualify them to draw a price/budget line or budget constraint. Therefore, the ICs tell us what choices the household would like to make and the price/budget line or budget constraint tells us what the household can do.
It means indifference curves show consumers’ willingness to buy. IC does not tell anything about the consumer’s buying power. To determine how much of each good or service’s consumer purchases, we have to account for the consumer’s income and the relative prices of the goods. With the help of such information, we will be able to construct the budget/price line of a consumer.
In an indifference curve map, an upper indifference curve confirms a higher level of satisfaction than a lower one. Thus, a consumer in his attempt to maximize his satisfaction will try to reach the highest possible indifference curve. But in his chase of buying more and more goods and thus locating more and more fulfillment, he has to slog under two constraints.
- The buyer has to pay the prices for the goods and,
- He has a restricted amount of money income to buy the goods
Thus, how far he would go to buy goods he desired to have based on the prices and money income available to him. The money income available to the consumer is always can be represented with the help of a budget/price line or budget constraint.
A budget/price line or budget constraint shows all the blends of commodities that can be purchased with a given level of income of the consumer and the prices of the commodities.
According to John P. Gould and Edward P. Lazear, ‘The budget line is the set of commodity bundles that can be purchased if the entire money income is spent. Its slope is the negative of the price ratio’.
The budget/price line is the budget constraint of a consumer. So, it is the locus of the combinations of two goods that can be purchased under the given budget. Any combination lying on the budget line can be purchased by the consumer with his budget constraint. It is one of the significant tools used in the analysis of consumers’ equilibrium under ordinal utility analysis.
Construction of Price/Budget Line or Budget Constraint
Suppose the available money income is Rs. 100, the price of good-X (PX) is Rs. 20 and that of good-Y (PY) is Rs. 10. The following schedule shows the possible quantities of purchase from the given money income and prices of the goods.
| Combination | PX | QX | PXQX | PY | QY | PYQY | Total Budget |
| A | 20 | 0 | 0 | 10 | 10 | 100 | 100 |
| B | 20 | 1 | 20 | 10 | 8 | 80 | 100 |
| C | 20 | 2 | 40 | 10 | 6 | 60 | 100 |
| D | 20 | 3 | 60 | 10 | 4 | 40 | 100 |
| E | 20 | 4 | 80 | 10 | 2 | 20 | 100 |
| F | 20 | 5 | 100 | 10 | 0 | 0 | 100 |
If we plot the above schedule into the graph, we will get a downward sloping straight line budget/price line or budget constraint at given income and prices of goods. The following figure shows the budget line or budget constraint of a consumer.
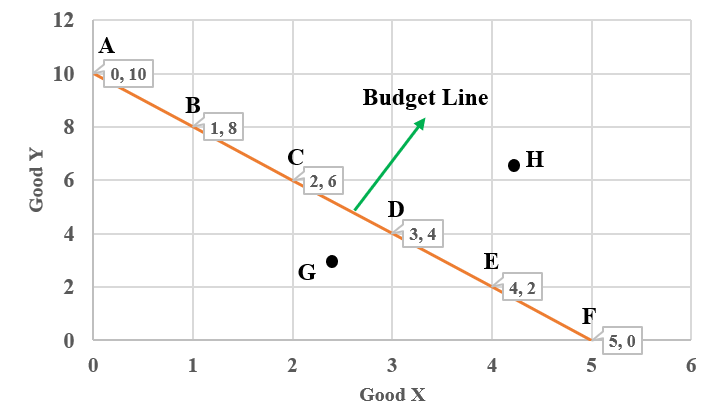
The above figure shows the budget/price line or budget constraint. For the easiest derivation of the budget line, first of all, we have to find two endpoints where the consumer consumes only one good. In the above figure point, A and E are two endpoints. At point A we can assume that the consumer consumes or spends all his income on the purchase of good Y only with zero units of good X.
Likewise, at point F, we can assume that the consumer has spent all his income on the purchase of good X and there are zero units of good Y. The intermediate points, B, C, D, and E include various combinations of good X and Y both.
Point G lies inside the budget line and can be considered an inefficient point. It is because at point G the consumer is not spending the entire amount of money income available to him. The efficient choice is achieved only when expenditure is equal to the total available money income. Similarly, point H lies beyond the budget line and it is outside the existing capacity of the consumer. Here the expenditure is higher than the available amount of money income to the consumer.
Thus, given limited money income and prices of goods, the buyer is only able to purchase limited quantities of goods X and Y. Point B, C, D, and E represent the efficient choice where the expenditure is equal to the money income available.
Derivation of Equation of Budget/Price Line
The budget/price line of the budget constraint can be represented by an algebraic equation as well. Suppose that, M is given the amount of money income, PX is per unit price of good X, and PY is per unit price of good Y. Then from the given information a general form of the budget line is expressed as;
PX. QX + PY. QY=M
Where PX is the price of good X; PY is the price of good Y; QX is the quantity of good X; QY is the quantity of good Y, and M is money income available to the consumer. Similarly, PX. QX is spending on good X; and PY. QY is spending on good Y.
If the buyers purchase no units of good Y that are QY=0, then the maximum units of X can be bought by the consumer. The maximum units of good X can be calculated as; QX=M/ PX. This generates the X-intercept of the horizontal intercept of the budget line.
Similarly, if the buyers purchase no units of good X that are QX=0, then the maximum units of Y can be purchased by the consumer. The maximum units of good Y can be obtained by doing QY=M/ PY. This also generates the Y-intercept or the vertical intercept of the budget line.
In the above figure, point A shows the maximum units of good Y and generates the OA Y-intercept of the budget line AF. Likewise, point F shows the extreme units of good X as OF and this is the X-intercept of the budget line.
Example of Derivation of Budget Line
Let a consumer selects two goods J and T for consumption having a price of Rs. 200 and Rs. 100 respectively and a fixed income is Rs. 10,000. Draw the budget line.
Solution
The income of the consumer (M)= Rs. 10,000; the price of good J (PJ)= Rs. 200 and the price of good T (PT) =Rs. 100
Suppose the consumer has spent all the available income to purchase good J (i.e., QT=0). Now the units of good J that consumer can purchase is determined by;
QJ=M/PJ =10000/200= 50 units (X-intercept) and this gives us the combination (50,0)
Similarly, if the consumer spent his entire income on the purchase of good T (i.e., QJ=0). The unit of good T that the consumer can purchase is determined by;
M/PT=10,000/100= 100 units (Y-intercept) and this gives us the combination (0, 100)
Based on the calculated two combinations or two intercepts or the extreme values of horizontal/X-axis and vertical/Y-axis we can derive the budget line of the consumer with the help of a graph. The following figure/graph shows the budget/price line or the budget constraint of the consumer.

Therefore, the required equation of the budget line is 200QJ+100QT=10,000.
The slope of the Budget/Price Line or the Budget Constraint
Fundamentally, the slope of the budget line specifies how many units of one good (a good measure on the Y-axis) a customer must give up to purchase one more unit of another good (measured on the Y-axis) in the combination. In technical language, the slope of the budget line is equal to the negative of the ratio of the price of goods or services measured on the X-axis to the price of goods or services measured on the Y-axis. This can be obtained in an alternative way by taking a derivative of QY concerning QX.
Thus, the slope of the budget line is = -Yintercept/X intercept.
The slope of the budget line is always negatively sloped implying that given the level of income more is purchased if the price falls and less is purchased if the price rises. So, the slope of budget line AF is;
Slope of line AF=-OA/OF ={M/PY}/{M/PX} = -M/PY*PX/M=-PX/PY
We can measure the slope of the budget/price line or the budget constraint from the concept of the derivative. It is given by the derivative of QY concerning QX. That is, by the ratio of change in the number of goods measured on the vertical axis to the change in the number of goods measured in the horizontal axis. Then the equation of QY is;
QY=M/PY-PX/PY*QX (From the equation of the budget line)
Now differentiating QY concerning QX, we get
dQY/dQX= d(M/PY-PX/PY*QX)/dQX
So, dQY/dQX=-PX/PY
The slope may also be obtained by the total differential of the budget line as given below;
dM=d(PXQX+PYQY)
Or, dM= PX. d(QX) + PY. d(QY)
Or, 0= PX. d(QX) + PY. d(QY)
Or, -PX. d(QX) = PY. d(QY)
So, dQY/dQX = -PX/ PY
Thus, the slope of the price line is the ratio of the prices of two commodities. As we know that the prices are always positive, and the slope of the budget line is always negative. The negative slope of the price line indicates that, if the consumer wants to spend more money on one good then he has to sacrifice the money expenditure on other goods as available money income is constant.
Shift and swing in the Budget/Price Line or the Budget Constraint
The price line is designed based on the income of the consumer and the prices of goods in the market. If there is a change in the income of the consumer or in the prices of goods, the price line shifts in response to the change in these major factors. Here the change in income means to increase and decrease in income, assuming the price remains the same, and a change in price means a decrease or increase in the prices of the goods, assuming income remains the same.
Change in Income and its Effect on Budget Line
When there is a change in the income of the consumer, the prices of goods remain the same, and the price line shifts from the original position. The budget/price line or the budget constraint shifts outward to the right when there is a rise in income available to the consumer.
Similarly, with a fall in the level of income, and product prices remaining unchanged, the price line shifts to the left side from the original position. Thus, with a higher income, the consumer can purchase more of both goods than before, and with a fall in income, the buyer will not able to purchase the quantity that he was purchasing before. The following diagram shows the rightward as well as a leftward shift in price line as a result of the increase and decreases in income respectively, assuming prices remain the same.

The above figure shows the shift in the price line as a result of the change in income available to the consumer. The increase in income, (assuming the price remains the same) has resulted in a rightward shift in the budget line from AB to A1B1. With a new budget line, now the consumer can purchase more of both the goods J and T.
Similarly, when there is a decrease in the income of the consumer, assuming the same, the result will bring a leftward shift in the budget line. As the figure has shown the leftward shift of the budget line from AB to A2B2, is due to a decrease in the money income available to the consumer. Now with such a fall in income, the consumer is not able to purchase the quantities of goods J and T as much as he was purchasing before the change of such income.
Thus, when there is a change in the income of the consumer, the prices of goods remain the same, and the price line shifts from the original position.
| Factors | Initial Case | Decreased Case | Increased Case |
| Income | 10,000 | 5,000 | 15000 |
| Price of Good J | 200 | 200 | 200 |
| Price of Good T | 100 | 100 | 100 |
| Price Line | AB | A2B2 | A1B1 |
Here in the table, we can see the change in the income of the consumer assuming the prices of Good J and T remain the same and its effect on consumers’ ability to purchase such goods.
Change in Price and its Effect on Budget Line
Change in price (income remaining the same) also brings the rotation in the budget line. Here the change in price may have been seen from two different angles. First, there is the non-proportional change in price and the second is the proportional change in price.
Non-proportional or Disproportional Change in Price
Suppose that the price of the goods has changed and income remains the same. More specifically, when there is a change in the price of one commodity, assuming the price of other commodities and the income of the buyers remains the same. It is the case of a non-proportional change in price. The budget line will rotate or swing inward or outward with the change in the price of only one good, and no change in the price of other goods and the consumer’s income.
An increase in the price of the commodity measured along the X-axis brings inward rotation in the price line and a decrease in the price of the same causes the budget line to rotate towards the right.
The following figure shows the effect of change in the price of the commodity measured along the X-axis on the price line or the budget line.

The above figure has shown the effect of non-proportional change in the price of good J on the price line. When there is a decrease in the price of Good J, the real purchasing power of the consumer has increased and now he can buy more commodities of Good J. This will swing the price lone towards the right. Similarly, in case of an increase in the price of good J, the budget line will swing towards the left. This has been shown by the swing of the price line from AB to AB1 and AB2 respectively.
| Factors | Initial Case | Decreased Case | Increased Case |
| Income | 10,000 | 10,000 | 10,000 |
| Price of Good J | 200 | 133.33 | 400 |
| Price of Good T | 100 | 100 | 100 |
| Price Line | AB | AB1 | AB2 |
Here in the table, we can see the non-proportional change in the price (change in the price of Good J) and its effect on consumers’ ability to purchase such goods.
Proportional Change in Price
When there is an increase or decrease in the price of both goods by the same proportion then it is the case of a proportional change in price. in such a case, there is a shift in the budget line parallel to the initial shape. The slope of the budget line in such a case does not change. If the price of both goods rises by the same proportion, the budget line will shift inward and if the price of both goods falls proportionally, the budget line shifts outward. In this case, we assume the income of the consumer remains the same and only there is a proportional change in the price of both goods. The following diagram shows the effect of the proportional change in the price of both of the goods in the price line.

Here, AB is the initial budget line. When there is an increase in the price of goods J and T proportionally, the price line will shift to A2B2 from AB. Similarly, if the price of both goods falls proportionally, the budget line shifts to the right position A1B1.
| Factors | Initial Case | Decreased Case | Increased Case |
| Income | 10,000 | 10,000 | 10,000 |
| Price of Good J | 200 | 133.33 | 400 |
| Price of Good T | 100 | 66.66 | 200 |
| Price Line | AB | A1B1 | A2B2 |
Here in the table, we can see the proportional change in the prices of Good J and T and its effect on consumers’ ability to purchase such goods.
References and Suggesting Readings
Ahuja, H.L. (2017). Advance Economic Theory. New Delhi: S. Chand & Company.
Dhakal, R. (2019). Microeconomics for Business. Kathmandu: Samjahan Publication Pvt. Ltd.
Dwivedi, D. N. (2018). Microeconomics Theory and Application. New Delhi: Vikas Publishing House PVT LTD
Kanel, N.R. and et. al. (2019). Microeconomics for Business. Kathmandu: Buddha Publications.
Shrestha, P.P. and et. al. (2019). Microeconomics for Business. Kathmandu: Advance Saraswati Prakashan.